Obecný úvod k laboratorním cvičením z fyziky

Doc. Miloš Steinhart 15. 10. 2018 909. 08. 2016; 24. 02. 2009; 08. 12. 2006 poznámky na konci)

!!! Pozor, na textu se pracuje. Bude hotov na začátku letního semestru!!!

!!! Při převodu z formátu WORD do html se některé grafické prvky hlavně horní a spodní indexy neprovedly správně a čísla rovnic nejsou na konci řádků, ale nalepena na rovnice. Zatím též nejsou převedeny všechny obrázky. Přesto se domnívám, že text je srozumitelný. Budu na něm dále pracovat. Zobrazuje-li se nesprávně s a z s háčkem, přepněte zobrazit/kódování na středoevropské ISO-8859-2. MS !!!

Úvod
Chyby systematické a náhodné
Správnost měření
Přesnost měření
Základy statistického zpracování výsledků
Přiklad zpracování výsledků
Závěrečné poznámky

Obsah Předchozí Další

Úvod - proč se chybami vůbec zabýváme?

Fyzika je věda založená na experimentu. Tato skutečnost obvykle uniká posluchačům, protože musí při studiu jejích základů rychle vstřebat značné množství informací. Při fyzikálním poznávání světa sledujeme určitý jev. Snažíme se jej kvantifikovat a vytvořit si o něm jistou představu. Ta je vyjádřena modelem, zpravidla matematickým. Za určitou dobu se obvykle stává, že přesnější měření vyvrátí zavedené představy a vynutí si vytvoření nových teorií. Těch často bývá větší množství a liší se modely a předpoklady, na kterých jsou postaveny. Jinak všechny mají zpravidla správnou vnitřní logickou stavbu. Přežije z nich ale jen ta, která není v rozporu s výsledky experimentu. Tím se také (dočasně) potvrdí její předpoklady. Pokud je i takových teorií více, rozhodne o tom, která z nich je skutečně správná opět nový, kvalitnější experiment.
Slavný fyzik Richard P. Feynman to velice výstižně charakterizoval slovy, že exaktní vědy jsou takové, v nichž výjimka nepotvrzuje pravidlo, ale vyvrací jej. Podobně Stephen Hawking přirovnává teorii k modelu loďky, který muže mít mnoho zajímavých vlastností, ale nakonec buď plave nebo neplave.

Smyslem laboratorních cvičení z fyziky je, aby si posluchači v praxi ověřili platnost některých důležitých fyzikálních zákonů, naučili se provádět základní fyzikální měření a vyhodnocování jejich výsledků a poznali nejběžnější měřící přístroje. Neméně důležité je, aby se na relativně jednoduchých měřeních naučili rozvíjet základní experimentální cit. Ten je založen na hlubokém uvědomování si kvalitativních i kvantitativních aspektů příslušného měření. Především to znamená zamýšlet se nad použitými metodami, jimi získanými výsledky a jejich přesností. Experimentální cit je nadčasový a neztratí v žádném případě význam ani u budoucích moderních technik. Ty jistě zrychlí experiment a zkvalitní jej po mnoha stránkách, avšak na druhé straně bude vlastní princip měření více a více skryt v důsledku komplikovanosti elektroniky, výpočetní techniky a často dokonce i záměru výrobců přístroje.

Význam přesnosti měření ilustruje velmi mnoho příkladů z historie, kdy lépe provedený experiment zbořil třeba i dlouho všeobecně uznávané a základní představy o světě. Za všechny uveďme známý Michelsonův pokus z roku 1887. Jím bylo dokázáno s dostatečnou přesností, že rychlost světla je stejná alespoň ve dvou souřadných soustavách, které se navzájem rovnoměrně pohybují. Tím byla navždy vyvrácena představa, že se rychlosti skládají podle Galileovy transformace a že ve všech soustavách běží jeden univerzální čas. O platnosti těchto představ neměl do té doby nikdo sebemenší důvod pochybovat. Michelsonův pokus je navíc příkladem negativního experimentu. Původně měl totiž dokázat unášení světla éterem, a to přes veškerou snahu a pečlivost naopak vyvrátil.

O nutnosti měnit dosavadní teorii rozhoduje to, zda hodnoty, které předpovídá, jsou novými měřeními vyloučeny. To znamená, zda jsou nepochybně vně intervalu daného přesností měření, tzv. chybového intervalu.
Obecně by tedy měla platit zásada, že každý výsledek experimentu, který se má brát važně, se musí uvádět vždy včetně odhadu své přesnosti. Je tedy nutné umět tuto veličinu určit u každé naměřené hodnoty. U nepřímo měřených veličin, tedy těch, které jsou z naměřených hodnot vypočítávány, je navíc nutno znát zásady, jakým způsobem chyby pronikají do výsledku při matematickém zpracování.

Cílem tohoto textu je poskytnout základy postupů zpracování měření. To zahrnuje znalost toho, jaké hlavní druhy chyb existují, jakým způsobem se snažíme určovat jejich velikost a jak je popřípadě minimalizovat. Bez důkazů uvádíme některé důležité závěry ze statistiky a snažíme se ilustrovat, jak se správně používají. Podrobnější rozbor statistických metod najde čtenář v řadě klasických učebnic. S nimi se posluchači jistě seznámí při dalším studiu. Zde se intenzívně věnujeme také systematickým chybám, jejichž vliv bývá často podceňován.

Obsah Předchozí Další

Chyby systematické a chyby náhodné

Žádná hodnota získaná měřením není obecně přesně rovna měřené veličině, nýbrž je vždy získána s jistou odchylkou a to i v případě, že neuvažujeme hrubé chyby a lidský faktor. Výrazy odchylka nebo chyba budeme používat jako synonyma a rozumíme jimi vzdálenost od správné hodnoty.

Odchyky lze rozdělit do dvou hlavních skupin na systematické a náhodné. V anglosaské literatuře se pro vzdálenost od správné hodnoty, způsobenou systematikými vlivy, používá výraz accuracy a pro vzdálenost způsobenou vlivy náhodnými, výraz precision. Aby i v češtině bylo jasné, o jaký druh chyby jde, snaží se někteří autoři používat jako ekvivalenty výrazy správnost respektive přesnost. Bohužel v řadě ustálených termínů se často užívá v obou případech tradičně slova přesnost. Navíc zápor nesprávnost obvykle nemá zamýšlený význam. V tomto textu se nicméně budeme o rozlišení na správnosti a přesnosti snažit všude, kde to bude možné.
Toto rozdělení chyb není samoúčelné. Obě skupiny odchylek se vyznačují různými vlastnosti a abychom odhadli jejich velikost, popřípadě je v co největší míře minimalizovali nebo dokonce (efektivně) odstranili, musíme postupovat jiným způsobem. Obor, který se zabývá tím, jak optimálně naplánovat experiment z hlediska minimalizace vlivu chyb a případných nákladů se nazývá strategie měření. S vyhodnocováním měření, jímž se zde zabýváme především, samozřejmě úzce souvisí.

Charakter obou druhů odchylek lze velmi názorně ilustrovat pomocí terče, do něhož stříleli dva střelci podle obr. 1 . Zásahy prvního střelce jsou označeny zelenými "+" a druhého červenými "x". Pro každou skupinu zásahů jsme nalezli odhad středního zásahu jako těžiště a odhadli rozptyl jako kruh, který obsahuje polovinu zásahů a má střed v tomto těžišti. Je označen jako "*" příslušné barvy.
Je zřejmé, že druhý střelec je lepší, protože jeho zásahy jsou od svého těžiště méně rozptýleny. Na druhé straně jeho těžiště je více vzdáleno od středu terče, což svědčí o tom, že jeho zbraň více zanáší. Zanášení pušky je chybou systematickou, zatímco odchylka jednotlivých zásahů od středního zásahu je chybou náhodnou.

Obtížnost reálných fyzikálních měření spočívá v tom, že se vlastně snažíme z jednoho nebo několika zásahů najít střed terče. Přitom se oba druhy odchylek, podobně jako při střelbě, vyskytují současně. Oba se také promítají do případného výpočtu dalších veličin, kam bychom měli dosadit správnou hodnotu (střed terče).
Pro snažší pochopení charakteru obou druhů odchylek je však napřed budeme uvažovat odděleně.

Obsah Předchozí Další

Správnost měření a chyby systematické

Typický příklad experimentu, zatíženého systematickou odchylkou, je měření odporu metodou přímou podle obr. 2 . Je zřejmé, že ani při sebevětší přesnosti přístrojů ani při libovolném počtu opakovaných měření, neobdržíme správnou hodnotu napětí, kterou potřebujeme pro výpočet odporu R podle Ohmova zákona. Vždy naměříme více o napětí na ampérmetru. Ten totiž není ideální a jeho vnitřní odpor R_A tedy není nulový. Poměr naměřeného napětí a proudu bude roven součtu R+R_A. Kdybychom vnitřní odpor R_A znali, snadno bychom hodnotu každého neznámeho odporu R vypočítali. Na odstranění systematické chyby tedy stačí určit v našem případě jeden parametr - R_A. Ten můžeme nalézt experimentálně, například když uskutečníme navíc minimálně jedno měření, při kterém bude na místě neznámého odporu rezistor známé hodnoty (nejlépe přesný odpor - normál).

Zobecníme tento postup: V první řadě je nutné analyzovat experiment a umět odhadnout příčiny systematické chyby, její velikost a počet parametrů, jimiž ji lze popsat. Hodnotu těchto parametrů potom zpravidla určujeme kalibrací, proměřením jednoho nebo několika známých vzorků (standardů). Minimální počet kalibračních měření je dán počtem příslušných parametrů. Pomocí nich následně provádíme korekci měření na vzorcích neznámých. Výsledná systematická chyba přitom bude dána přesností kalibrace. Proto provedení více kalibračních měření, než je nutné minimum, není na závadu.

Při běžném měření aplikujeme známou metodu na neznámý vzorek, abychom se něco dozvěděli o něm. Kalibrace je speciální experiment, zvláštní v tom, že měříme známý vzorek s cílem získat informace o použité metodě.

V rámci řešení laboratorních úloh budeme provádět řadu kalibrací.
Například při určování měrného tepla  látek spočívá systematická chyba v tom, že určité tepelné energie je potřeba k zahřátí samotné vnitřní nádoby kalorimetru, míchadla a teploměru, i když jsou jinak dokonale izolovány od okolí. Tuto odchylku stačí kvantifikovat jedním parametrem - tepelnou kapacitou kalorimetru. Pro její určení stačí provést navíc jediné měření. Při něm se v přístroji smísí dvě známá množství látky, obvykle vody, o známém měrném teple a různé teplotě.
Podobně s jedním kalibračním měřením vystačíme při měření velkých odporů  pomocí vybíjení kondenzátoru. Zde je nutné určit velikost svodového odporu, který způsobuje vybíjení i v případě, že kondenzátor není přemostěn žádným vnějším (měřeným) rezistorem.

Časté jsou situace, kdy je nutno určit kalibračních parametrů více. Například z teorie (opět podložené experimenty) víme, že dispersní křivka spektrometru   je v dobrém přiblížení křivkou druhého řádu. Pro její určení tedy musíme proměřit minimálně tři známé spektrální čáry. Není ale na škodu jich změřit více, protože to vede, vzhledem k současnému výskytu odchylky náhodné, ke zpřesnění kalibrace. Obvykle ale vystačíme s jedním standardem, který má více vhodných spektrálních čar.

K nejobtížnější situaci dochází, není-li počet parametrů (stupňů volnosti) problému znám. Zde je nutno proměřit větší množství kalibračních vzorků a použít postupů faktorové analýzy. V jednodušších případech je možné odhadnout kalibrační závislost z grafu nebo přesněji použitím regresních metod. Například u kalibrace tónového generátoru  nebo kalibrace galvanometru  docházíme k lineárním závislostem.

Správný odhad velikosti systematické chyby nám umožní posoudit, zda je významná či nikoli. Kritériem je, zda je možné ji zanedbat vzhledem k přesnosti měření.
Puška prvního (zeleného) střelce je s ohledem na jeho střelecké umění celkem vyhovující a dávat mu lepší zbraň by bylo mrháním. Kdežto druhý střelec by lepší zbraň potřeboval.
Při měření rezistoru podle našeho příkladu je pro podobné posouzení potřeba znát vnitřní odpor ampérmetru R_A, přesnost použitého voltmetru a alespoň přibližně velikost hledaného odporu R.

U komerčních měřících přístrojů obvykle provádí kalibraci výrobce a uvádí příslušné parametry a grafy v dokumentaci.
Přesnost přístrojů se obvykle vyjadřuje pomocí třídy přesnosti δ_p. Tou se rozumí podíl maximální odchylky Δ_max přístroje k maximu daného rozsahu (stupnice) X_max

1.

Udává se obvykle v procentech, přičemž se symbol % neuvádí. Naměříme-li na takovém přístroji hodnotu X, je její relativní odchylka

2.

Třída přesnosti je tedy minimální relativní chyba, jakou lze s přístrojem dosáhnout a to tehdy, když je výchylka X u ručkových přístrojů co nejblíže hornímu okraji stupnice nebo u digitálních maximální hodnotě příslušného rozsahu.
Z toho plyne, že když můžeme změřit jistou veličinu na několika rozsazích, volíme z hlediska správnosti měření vždy ten nejcitlivější z nich. Digitální přístroje s automatickým přepínáním rozsahů provádějí tuto volbu samy. U kvalitnějších z nich je možné mimoto nastavit rozsah podle potřeby i ručně. To je užitečné například, když je žádoucí, aby se proměření určité série hodnot provedlo na stejném rozsahu. Změna rozsahu, totiž vede ke změně vnitřního odpor přístroje a tím může ovlivnit poměry v měřeném obvodu a tím i zjišťovanou závislost. Významné to je zvláště při měření proudu, a to i u digitálních multimetrů, používaných v naší laboratoři.

Používáme-li například voltmetr třídy přesnosti 1.5, je zřejmé, že pro R > 500R_A, bude systematická chyba stanovení napětí pod jeho rozlišením a tudíž se neprojeví. Avšak bude-li např. R < 50R_A bude přístroj schopen napětí na ampérmetru zaregistrovat a jeho údaj bude tedy nesprávný. Pro měření větších odporů je tedy zapojení podle obr. 2  vyhovující.
Například u běžného ampérmetru na rozsahu 20 mA, může být R_A až několik ohmů. To je od nuly dosti daleko. Přesto odpory o velikosti řádově několik kΩ změříme správně.

Informace o významnosti systematické chyby je též možné získat srovnáním s výsledky jiné měřící metody. V případě měření odporů metodou přímou můžeme například použít zapojení podle obr. 3 . I zde se ovšem dopouštíme systematické chyby. Tentokrát při měření proudu, protože ampérmetr měří současně proud neznámým odporem i voltmetrem. Rozborem zjistíme, že metoda je vhodná pro měření odporů mnohonásobně menších, než je vnitřní odpor voltmetru. Je-li i v tomto zapojení systematická chyba signifikantní, získáme každopádně lepší představu o skutečné hodnotě odporu díky faktu, že první zapojení poskytuje vždy horní odhad R, zatímco druhé zapojení odhad spodní. Je ale nutné zdůraznit, a ilustruje to i náš příklad s terčem, že zde se jedná o vyjímečně příznivý případ, kdy každá "puška" zanáší přesně na opačnou stranu. Ovšem i zde nesymetricky!
Obecně není zaručeno, že správná hodnota leží mezi hodnotami naměřenými různými metodami a samozřejmě ani jejich aritmetický průměr nemusí být ke správné hodnotě blíže než některé z měření a má proto smysl pouze orientační. Je-li například jedno měření téměř správné ovlivní ostatní nesprávná měření průměr nevhodně. Příkladem je měření velkého odporu v zapojeních obr. 2 a 3. V prvním zapojení dostáváme téměř správnou hodnotu a její zprůměrování s hodnotou ze zapojení druhého dá nesmyslný výsledek.

Typickým příkladem, kdy aritmetický průměr nemá smysl, je měření specifického náboje . Zde jsou jednotlivé hodnoty získány za různých podmínek a jsou tedy nutně ovlivněny systematickými vlivy. Například pro větší dráhy elektronů je magnetické pole méně homogenní. Podobně je nutné velmi opatrně iterpretovat průměr z několika postupů například u měření hustoty kapalin, ohniskové vzdálenosti tenkých čoček nebo odporu rezistorů. Ještě je nutné si uvědomit, že statistické balíčky nabízí různé postupy pro vyřazení odlehlých hodnot. Ale to funguje jen pro náhodné odchylky! Jedná-li se o chybu systematickou může být výsledek jedné metody zcela odlehlý od ostatních a přesto být nejsprávnější.

Běžné digitální přístroje, které používáme při našich laboratorních úlohách mají R_V = 10⁸ Ω, R_A = 1 Ω a třídu přesnosti 1.5. Mohlo by se zdát, že s nimi můžeme změřit přímou metodou správně odpory všech hodnot a ty v rozmezí 0.5 - 200 kΩ dokonce v obou zapojeních. Bohužel tomu tak není. Problematické je měření odporů příliš velkých a příliš malých. V prvním případě narážíme na obtížnost správně změřit velmi malé proudy a v druhém je měření zcela znehodnoceno odporem přívodních vodičů a přechodových odporem jejich kontaktů. Řešením je pouze použití speciálních postupů. Například již zmíněnou metodu měření velkých odporů vybíjením kondenzátoru nebo u malých odporů měření čtyřbodové obr. 3 , u kterého je vliv přívodních vodičů elegantně odstraněn.

Obsah Předchozí Další

Přesnost měření a chyby náhodné

Náhodné chyby jsou způsobeny velkým množstvím vlivů, které nejsme schopni přesně popsat a neznáme jejich příčinu. Důležité ale je, že obvykle můžeme předpokládat, že mají určité rozdělení. Často mají náhodné chyby takzvané rozdělení normální neboli Gaussovo. Je to důsledkem platnosti centrálního limitního teorému statistiky, který říká, že rozdělení systému, majícího velký počet stupňů volnosti, které mohou mít třeba i jiné než normální rozložení, konverguje k rozložení normálnímu.

Protože střední hodnota chyby je nula, lze vliv náhodných chyb principiálně ovlivnit opakováním počtu měření a statistika poskytuje metody, jak tyto chyby kvantifikovat.
Zhruba lze říci, že statistika nám umožňuje na základě rozumně malého počtu měření odhadnout, k jakým výsledkům bychom došli při počtu postatně větším (nekonečném). Její výpověď má charakter pravděpodobnosti a s roustoucím počtem uskutečněných měření se upřesňuje.

Příkladem je známá situace, kdy se na základě průběžných volebních výsledků v několika obvodech provádí odhad konečných výsledků voleb. Zde ale nestačí mít dostatečný počet respondentů. Vybrané obvody musí být navíc reprezentativní. Proto se výsledky různých průzkumů mohou značně lišit.

Honosné statistické zpracování by se nemělo používat k zakrytí myšlenkové prázdnoty [J. Fiala], nýbrž k vydolování maxima informace v měřeních obsažené (data mining).

V další poměrně obtížné části se snažíme vysvětlit, na jakých principech statistiké metody pracují. Je to v rozsahu, který umožní kvalifikovaně používat některé počítačové programy nebo kalkulátory, nabízející statistické funkce. Čtenářům doporučujeme ji podrobně prostudovat. K řadě definic a pojmům je možné se vrátit po pochopení ilustrativního příkladu na konci.

Obsah Předchozí Další

Základy statistického zpracování výsledků

Nejpropracovanější výsledky poskytuje statistika právě pro náhodné proměnné, mající normální rozložení. Začněme však obecnými pojmy.

Rozložení f(x) náhodné proměnnné x bychom teoreticky získali, kdybychom proměnnou nekonečněkrát změřili a vynesli křivku četnosti. Tedy závislost, jak často se proměnná vyskytuje v nekonečně malém okolí příslušných hodnot x bychom znormalizovali, tedy vydělili celkovým počtem měření, aby

3.

O proměnné x předpokládáme, že může nabývat jakékoli reálné hodnoty. Rozdělení f(x) potom vyjadřuje skutečnost, že určité hodnoty x se vyskytuji častěji než jiné. Snadno se to ilustruje na proměnných nabývajících diskrétních hodnot. Házejme dvěmi kostkami a ať je naše proměnná součtem hodnot, které padly. Proměnná může nabývat všech celých hodnot v intervalu <2,12>. Ale například součtu 2 bude dosaženo jen při jedné z 36 možných konfigurací(1+1), podobně jako součtu 12 (6+6). Ale třeba k součtu 6 dochází při pěti konfiguracích (1+5, 2+4, 3+3, 4+2, 5+1). Hodnota f(6) tedy bude pětkrát větší než f(1).

Hodnotu f(x) lze chápat jako pravděpodobnost výskytu náhodné proměnné v malém okolí x, v intervalu <x, x+dx>. Potom pravděpodobnost p výskytu proměnné x mezi hodnotami x₁ a x₂ je

4.

Pro každé rozdělení existuje jednoznačná kumulativní neboli distribuční funkce F(x)

5.

Jejím oborem hodnot je interval <0,1>. Má význam pravděpodobnosti, že náhodná proměnná dosáhne hodnoty menší nebo rovné x. Zjevně platí obdoba rovnice(4):

p(x₁ < x < x₂) = F(x₂) - F(x₁)

Velmi důležitá je zvláště inverzní úloha: pro jakou hodnotu x_p, bude F(x_p) = p. Hodnota x_p se nazývá kvantil, odpovídající pravděpodobnosti p.

Na obr. 4  je ilustrován význam některých důležitých kvantilů: mediánu - x_0.5, horního kvartilu - x_0.75 a horního decilu - x_0.9 u obecného nesymetrického rozložení. Hodnoty kvantilů jsme snadno nalezli vpravo pomocí distribuční funkce, jak je naznačeno červenými šipkami a přenesli doleva na rozdělení pravděpodobnosti, na němž jsou navíc vyznačeny další důležité body: maximum funkce - modus, střední hodnota a střední kvadratická hodnota .
Dříve byly právě tabelované hodnoty kvantilů nejdůležitějším zdrojem informací o příslušných rozděleních. V současné době jsou kvantily dostupné v mnoha matematických programech na počítačích jako inverzní hodnota distribuční funkce nebo přímo jako kvantilová funkce.

Úplnou informaci o chování náhodné proměnné poskytuje pouze znalost rozdělení v celém jeho definičním oboru. Řadu konkrétních důležitých rozdělení je ale možné plně nebo alespoň s dostatečnou přesností charakterizovat několika parametry. Klíčem pro jejich definici je takzvaná střední hodnota. Je-li g(x) funkce náhodné proměnné x, potom její střední hodnotu <g(x)> lze vyjádřit jako

6.

Speciálním případem jsou nejdůležitější parametry každého rozdělení, jeho střední hodnota μ

7

a dále takzvané obecné momenty α_r a centrální momenty μ_r

8.

Není-li funkce f(x) normovaná, je nutné vztahy pro výpočet momentů dělit výrazem.

Ve statistice jsou nejdůležitější první obecný moment α₁ = μ a druhý centrální moment μ₂.
V podrobnějších pracích se dokazuje, že každé rozdělení lze vyjádřit jako rozvoj jeho momentů. Ten může být základem pro odvození vlastností rozdělení veličin, které jsou speciálními funkcemi náhodných proměnných.

Jsou-li například x a y náhodné proměnné a a, b, c konstanty, platí

9

a jsou-li x a y navíc nezávislé, je

10.

Dále se budeme soustředit již jen na náhodné proměnné, které mají normální rozložení definované vztahem

11.

Lze ukázat, že rozdělení G splňuje normalizační podmínku (3), μ je jeho střední hodnota (tradiční označení je ve shodě s 7) a takzvaná variance σ² = μ₂ je jeho druhým centrálním momentem. Přitom její druhá odmocnina, standardní odchylka σ, má význam pološířky rozdělení (tedy jeho šířky v poloviční výšce).

Na obr. 5 jsou rozdělení G(μ, σ; x) s několika parametry a jim odpovídající distribuční funkce F(μ σ; x).

Pokud je μ=0, mohou odpovídat rozdělením náhodných chyb několika různých veličin. Jsou patrny nejdůležitější vlastnosti:
1) střední hodnota je 0
2) rozdělení jsou symetrická
3) pravděpodobnost velkých chyb se asymptoticky blíží 0
4) pološířka σ souvisí s přesností samotné veličiny, např. vlivu fluktuací

Chápeme-li rozdělení jako pravděpodobnost, je zřejmé, proč je rozdělení odpovídající menšímu σ přesnější. Menší chyby jsou u něj totiž více pravděpodobné a větší méně..

Ze zobrazení normalizovaného normálního rozdělení a jeho distribucni funkce je patrné, ze pravděpodobnost, že náhodná proměnná x bude v intervalu μ±σ je

12.

Obdobně lze ukázat pravděpodobnost, že hodnota měření bude v intervalu μ±2σ a μ±3σ je 0.9554 resp. 0.9974.

Parametry μ a σ plně charakterizují normální rozdělení náhodné veličiny x. Jsou to také veškeré informace, potřebné pro použití veličiny v dalších výpočtech. K jejich přesnému určení by ovšem bylo nutné uskutečnit nekonečný počet měření.

Z praktických důvodů měření opakujeme pouze n-krát, čimž z náhodného rozložení provádíme takzaný výběr o rozsahu n (x₁, x₂ ... x_n). Jedním z hlavních cílů teorie pravděpodobnosti je aproximovat parametry μ a σ rozdělení náhodné veličiny x pomocí parametrů získaných z výběru, takzvaných statistik.
Lze ukázat, že nejlepším odhadem střední hodnoty μ rozdělení je výběrový průměr

13.

a nejlepším odhadem variance σ² je výběrový rozptyl

14.

Jeho odmocnina s se nazývá střední chyba jednoho měření. Kdybychom mohli měření opakovat nekonečně krát, znali bychom přesně rozdělení a z těchto vztahů (pro nekonečné n) bychom získali přesné hodnoty výrazů μ a σ.

Pro konečný počet měření nám statistické metody umožňují pouze nalézt intervaly, kde skutečné hodnoty μ a σ leží na určité hladině věrohodnosti.. To se prakticky provádí pomocí takzvaných výběrových rozdělení Studentova a Pearsonova. Platí totiž, že náhodná veličina, obsahující μ

, 15

má takzvané Studentovo rozdělení s m=n-1 stupni volnosti a náhodná veličina, obsahující σ

, 16

má rozdělení Pearsonovo neboli χ² (chí kvadrát) s m stupni volnosti.

Přesná vyjádření těchto výběrových rozdělení je možné nalézt v podrobnější literatuře a pro praktické použití je není nutno znát. I tato rozdělení jsou nyní dostupná v řadě matematických programů. Je ale důleité vědět, že závisi také na rozsahu výběru. Zde ukážeme na příkladu simulovaného měření jejich použití podrobněji. Ukáže se také, v jakém smyslu je měření, opakované vícekrát, přesnější.

Obsah Předchozí Další

Příklad zpracování výsledků

Předpokládejme, že měřená veličina má normální rozložení G(20,3;x). Vygenerujme dva výběry o rozsahu 17 a 1700. Ty pro nás reprezentují dvě sady, krátkou a dlouhou, opakovaných měření. Nyní se snažme učinit odhad μ a σ na hladině věrohodnosti 68%, 95% a 99%.
Ukážeme si podrobně postup výpočtu pro rozsah n=17 a hladinu věrohodnosti 95%.

Hodnoty náhodné proměnné jsou v tabulce I. Podle rovnic 13 a 14 vypočteme výběrové parametry: aritmetický průměr a výběrový rozptyl  .

V dalším kroku určíme interval, v němž se vyskytuje střední hodnota rozdělení m na hladině věrohodnosti 95%. Podle rovnice 15 k  tomu potřebujeme znát oblast Studentova rozdělení pro počet stupňů volnosti m=n-1=16, která má obsah (integrál) 0.95. Ta je ohraničena sdola kvantilem t_0.025 a shora kvantilem t_0.975, jak je patrné z obr. 6 . Z tabulek nebo pomocí matematického programu zjistíme, že hodnoty kvantilů jsou t_0.025 = -2.12 a t_{0  .975} = +2.12 (Studentovo rozdělení je symetrické). Vyřešíme rovnici

a přes úpravu

17

dojdeme k nerovnosti 19.32 < μ < 21.82.

Protože se jedná o simulovaná data a my víme, že μ = 20, můžeme ověřit, že v intervalu, který jsme vypočítali, μ skutečně leží. Kdybychom ale tuto simulaci mnohokrát opakovali, zjistili bychom, že v 5% případů μ v daném intervalu ležet nebude. V tom spočívá význam hladiny věrohodnosti.

Analogicky postupujeme například pro odhad μ na hladině věrohodnosti 99%. Akorát použijeme kvantily t_0.005 = -t_0.995=-2.92 a dojdeme k nerovnosti 18.84 < μ < 22.3. Je pochopitelné, že vyjdeme-li ze stejných dat a chceme větší "jistotu", že střední hodnota v daném intervalu leží, musí být tento interval širší.

Obdobně postupujeme při odhadu intervalu pro varianci σ² rozložení podle rovnice 16. Nyní používáme rozložení Pearsonovo pro m=n-1=16 podle obr. 7. Opět najdeme příslušné kvantily χ_0.025 = 6.91 a χ_0.975 = 28.845. Pomocí hodnoty s vypočteme součet kvadrátů odchylek

  a řešíme rovnici

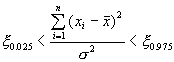  . Po úpravě obdržíme nerovnost 3.31 < σ² < 13.83.
Opět můžeme ověřit, že hodnota použitá při simulaci σ² = 9, ve vypočteném intervalu leží. Obdobně by tomu bylo v 95 % případů z velkého počtu simulací.
Pro hladinu věrohodnosti 99 % použijeme stejná rozložení, ale určíme kvantily t_0.005 , t_0.995 respektive χ_0.005 , χ_0.995.
Pro zpracování druhé sady dat o rozsahu 1700 je nutné použít rozdělení pro m = 1699. Jinak je postup obdobný.

Z tabulky II, kde je odhad μ a σ na hladině věrohodnosti 95 % a 99 % pro výběry obou rozsahů, jsou patrné další důležité závěry:

Z uvedeneho příkladu vyplývá, že pro odhad střední hodnoty rozdělení μ pomocí parametrů výběru o rozsahu n je významná tzv. standardní odchylka průměru nebo střední chyba aritmetického průměru s_x

18,

protože je rovna hodnotě koeficientu u kvantilů na obou stranách nerovnice 17. Tuto hodnotu tedy používáme k vyjádření chyby měření a veličinu získanou zpracováním výběru o rozsahu n zapisujeme jako

19.

I pro nepříliš velký rozsah výběru n leží v  68.3 % případů střední hodnota m v tomto intervalu. Plyne to z faktu, že kvantil t_0.1585~ -1 a ze symetrie Studentova rozdělení. Například: t_0.1585(3)=-1.2, t_0.1585(6)=-1.09, t_0.1585(10)=-1.05, t_0.1585(30)=-1.017.
Uvědomte si též souvislost s rovnicí 12.

Odchylka vyjádřená jako s_x má rozměr a jednotku měřené veličiny, a proto se nazývá chybou absolutní. Vztáhne-li se chyba k měřené hodnotě, lze ji vyjádřit pomocí bezrozměrné veličiny jako chybu relativní

20.

Pomocí této chyby je možné navzájem srovnávat měření různých veličin. Obecně platí, že měření s menší relativní chybou je přesnější. Tím je například odůvodněno známé tvrzení, že vážení je nejpřesnější měření.

V našem příkladě vychází s_n = 0.59 a d_x = 0.029. U méně přesných měření, kde d_x > 1 % uvádíme absolutní odchylku na jednu platnou číslici. Průměrnou hodnotu na tomto řádu zaokrouhlujeme. Výsledek našeho příkladu, kde je relativní chyba přibližně 3 %, bychom tedy zapsali x = 20.6 ± 0.6.

Absolutní a relativní vyjádření chyby má význam při odhadu odchylek veličin vypočítávaných pomocí veličin naměřených.

Předpokládejme, že náhodné veličiny x a y mají normální rozdělení, jsou na sobě nezávislé a platí

21.

Potom

22.

To plyne z vlastností normálního rozložení, kde a skutečnosti, že s je nejlepším odhadem parametru σ.

Je-li veličina z součinem nebo podílem nezávislých veličin x a y, tedy

23,

platí

24.

Oba vztahy je samozřejmě možné rozšířit na libovolný počet sčítanců, resp. činitelů.

Z rovnic 21 a 22 je také patrný problém metod, kde výsledek je rozdílem měřených veličin. Kriteriem přesnosti metody je totiž relativní chyba

25.

Jsou-li si hodnoty veličin x a y blízké, je jmenovatel malý a k dosažení uspokojivé přesnosti z je nutné změřit veličiny x a y s mnohem vyšší přesností, než kdyby se používaly samy o sobě.

Vyskytují-li se v součinu veličiny s vyšší mocninou, tedy například

26,

musí se využít obecnější vlastnosti rozptylu pro funkci z náhodných veličin x_i, kteté mají rozptyl σ_i a normální rozložení

27.

Po výpočtu příslušných derivací platí

28.

Odchylka veličiny s k-tou mocninou se tedy uplatní k-násobně a ne - násobně, jak by odpovídalo prosté aplikaci rovnice 24. Důvodem je skutečnost, že veličina x je sama se sebou korelována.

Obsah Předchozí Další

Závěrečné poznámky

Shrneme předchozí tvrzení.
Odolnost měření vůči náhodným chybám zvyšujeme zvětšením počtu měření a jejich statistickým zpracováním dokážeme odhadnout velikost odchylky výsledku. Pro odhalení vlivu odchylky systematické musíme provést kalibraci měření a jeho následnou korekci nebo použít srovnání několika různých experimentálních postupů.

U většiny reálných měření není hranice mezi systematickou a náhodnou chybou natolik ostrá, jak bylo popsáno, navíc předpoklad, že náhodné chyby mají normální rozložení, je nutné ověřit. Jediným správným soudem je analýza rozdělení naměřených hodnot kolem správné hodnoty. Pro ni bychom potřebovali provést nekonečně mnoho kalibračních měření. Reálné ale je provést konečný, ale dostatečně velký počet měření na známem vzorku. Statistika potom umožňuje extrapolovat vlastnosti výběrového rozdělení na rozdělení skutečné na určitém stupni věrohodnosti, jak bylo podrobně ukázáno na příkladu.

Je nutné si uvědomit, že náhodná chyba (, jejíž velikost odhadujeme např. pomocí s,) má dvojí příčinu: 1) v nepřesnosti měření a 2) ve fluktuacích měřené veličiny. Zvyšováním kvality experimentu a zpracování můžeme snižovat jen první z nich. Říkáme, že zvyšujeme rozlišovací schopnost měření. Pokud chceme například studovat velikost fluktuací, například proto, abychom ověřili určité závěry statistické fyziky, musíme provést měření dostatečně přesně, aby se náhodná chyba, způsobená fluktuacemi, neztratila v nepřesnosti měření.

Například, vážíme-li 100 krát jednu tužku, vypovídá statistické zpracování měření o kvalitě vážení, protože můžeme předpokládat, že fluktuace hmotnosti tužky je zanedbatelná. Zpracováváme-li ale vážení 100 různých tužek vypovídá statistické zpracování také o tom, jaké je rozdělení jejich hmotností, s jakou reprodukovatelností jsou tužky vyráběny. A právě opakované vážení jedné tužky umožní obě informace od sebe oddělit.

K podobnému příkladu fluktuace měřené veličiny dochází například při opakovaném měření průměru špatně opracovaného válečku, jehož obvod není přesná kružnice.

Při statistickém zpracování výsledků je tedy nutné srovnat výslednou odchylku s rozlišovací schopností měření, ale vzít v úvahu i citlivost měření. Kdybychom například vážili 100 tužek na kuchyňských vahách, mohli bychom snadno dojít k závěru, že jsou všechny tužky přesně stejné a výsledky statistického zpracování by k tomuto výsledku jednoznačně vedly jen proto, že rozdíly hmotností tužek by byly menší než rozlišovací schopnost vah.

V takovém případě musíme jako standardní odchylku pro další výpočet použít rozlišovací schopnost příslušného přístroje. Například u analytických vah 0.001 g, u velké šuplery 0.02 mm a u mikrometru 0.01 mm.

Obecně, je-li přesnost měření s_x srovnatelná s chybou přístroje Δ, je nutné výslednou odchylku vypočítat podle vztahu

29,

který plyne z rovnic 1, 2, 18 a 22.

U vědeckých experimentů je požadována reprodukovatelnost. Proto se v publikacích podrobně popisuje, jak a jakými přístroji byla měření prováděna.

Vznešené teorie, jako teorie supersrun, které o sobě a priori tvrdí, že jsou experimentálně neověřitelné, naopak nebudí ve velké části fyzikální komunity důvěru. To neznamená, že je chybná, ale jedná se nekonzistenci, jednu z mnoha na vrcholu pokroku, kterou bude potřeba v budoucnu odstranit.

***** Sem je to zhruba udělané. M.S. 16. 10. 2018 *****
 
  .

Tabulka I.

19.5410 19.0631 20.4183 22.7683 18.1377 20.2179

24.0228 21.2487 15.6172 20.2601 17.5074 22.3542

22.9094 19.7104 20.5752 19.7533 25.5580

.

Tabulka II.

rozsah věrohodnost 95% 99%

μ          17                       1700
68%  <19.98, 21.16> <19.85, 20.13>
95%  <19.31, 21.83> <19.85, 20.13>
99%  <18.84, 22.30> <19.80, 20.17>

σ <1.82, 3.72> <1.67, 4.31>

1700. μ <19.85, 20.13> <19.80,20.17>

Doporučená literatura:

1. J. Brož a kol. "Úvod do fyzikálních měření I", SPN Praha 1967
2. R. Košťál "Hodnoty a chyby veličin měřených a vypočtených", FO SPN 1972
3. International Table for Crystallography III,
4. M. Meloun a J. Militký "Statistické zpracování experimentálních dat", Plus Praha 1994
5. ....

Texty k obrázkům

Obr. 1

Ilustrace vlivu náhodné a systematické odchylky.

Obr. 2

Gausovo rozoložení chyb m=0, s = 3, 4 a 5.

Obr. 3

Studentovo rozložení pro m = 16 a 1699. Rozložení téměř splývají. U rozdělení m = 16 jsou vyznačeny kvantily, vymezující hladinu věrohodnosti 95%.

Obr. 4

Pearsonovo rozdělení pro m = 16. Jsou vyznačeny kvantily , vymezující hladinu věrohodnosti 95%.

Poznámky:

První odstavec - zvážit, kdy užít pojmu představa a kdy model - model vlastně nelze potvrdit absolutně, ale jen na určitém stupni poznání - tedy není nikdy potvrzen, ale časem je vyvrácen. Na druhé straně i překonaný model může za určitých okolností dostatečně fungovat, například relativistické efekty u pohybů pomalejších než dejme tomu 10 % rychlosti světla jsou prakticky zanedbatelné a lze prijmout klasický model jako první přiblížení. Ovšem například v případě přesné navigace nebo navádění řízených střel je třeba brát relativitu v úvahu i pro relativně pomalé pohyby. Je to otázka přesnosti.

aeiouue zscrdtn AEIOUUE ZSCRDTN

áéí úůě žščřřťň Ú Č