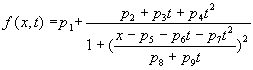
Využití kombinace genetického algoritmu s klasickou minimalizací
Miloš Steinhart
Ústav makromolekulární chemie AV ČR
Úvod
Obvyklým způsobem zpracování experimentálních dat je jejich fitování pomocí matematického modelu, jehož parametry mají určitý fyzikální význam. Pro tento postup je klíčové vytvořit model správný, tedy takový, který odpovídá měřenému jevu a zvolené metodě, a mít k dispozici spolehlivé fitovací procedury. Často, zejména u problémů s více stupni volnosti, se ukazuje, že i v případě, že mo
del dobře odpovídá uvedenému požadavku, klasické minimalizační metody na reálných datech selhávají. Důvodem je obtížnost určení správných hodnot startovacích parametrů, které tyto metody obvykle vyžadují. K jejich odhadu je nutné využít veškeré apriorní informace, která je k dispozici. Tou bývá v řadě případů jen rozpětí, v němž se hodnoty parametrů mohou nacházet. To může být i širší než jeden řád, což ke spolehlivému odhadu startovacích parametrů obvykle nestačí. Podobná situace nastává také, když matematický model nevystihuje přesně fyzikální situaci v celé její složitosti, ale jeho použití je jedinou rozumnou možností. V těchto případech se podle našich zkušeností osvědčuje využití metody genetického algoritmu[1], u níž je zadávání apriorní informace ve formě intervalu hodnot přirozené. Použití této metody pro úplné vypřesnění parametrů modelu je obtížné a zdlouhavé. Pro určení startovacích parametrů pro další klasickou minimalizaci je však tato metoda užitečná.Zde bude nejprve popsán princip metody genetického algoritmu a jeho propojení s klasickou minimalizační funkcí fmins, která je součástí Matlabu. Potom bude užitečnost metody ilustrována na třech typických příkladech z naší praxe[2].
Metoda genetického algoritmu a poznámky k funkci naprogramované v Matlabu
Metoda genetického algoritmu je založena na zakódování vypřesňovaných parametrů do bitového řetězce. V každé iteraci se zpracovává celý soubor řetězců, který se nazývá generací. Každý příslušník generace je použit k výpočtu testovací funkce. V ní se posuzuje podle určitého kriteria kvalita přiblížení se teoretické závislosti a experimentu. Řetězce se seřadí podle své úspěšnosti v testovací funkci. Nejlepší z nich se použijí jako rodiče a jejich kombinací (křížením) se vytvoří nová generace pro dalš
í iteraci. Tímto způsobem dochází k dědění pozitivních vlastností. Aby se zabránilo nebezpečí, že minimalizace bude ukončena v lokálním minimu, bývá nová generace před příslušnou iterací podrobena mutacím, při nichž dojde k náhodné výměně určitého malého počtu bitů. Tím se minimalizace přenese do jiného místa konfiguračního prostoru. V další iteraci se posoudí, zda příslušný skok byl oprávněný. V případě, že tomu tak není se výpočet vrátí do oblasti původní.Hlavní výhodou metody genetického algoritmu je její relativní necitlivost k volbě startovacích parametrů. Tato volba se uskutečňuje při procesu kódování, kde je každému parametru přiřazeno určité rozpětí hodnot a požadovaná přesnost. Tyto vlastnosti potom určují délku bitového řetězce jímž jsou všechny parametry dohromady reprezentovány a tedy také velikost příslušného konfiguračního prostoru.
Hlavní vlastnosti metody genetického algoritmu byly důkladně otestovány na simulovaných i experimentálních datech. Bylo zjištěno, že díky procesu dědění a přeskoků v konfiguračním prostoru konvergují parametry relativně rychle do blízkosti správných hodnot. Další zpřesňování je ale problematické protože proces dědění přestává být efektivní a náhodné mutace, které se stávají jediným mechanismem umožňujícím zlepšení, působí zároveň rušivě. Pravděpodobnost, že skok do jiné části konfiguračního prostoru povede ke zlepšení, v průběhu výpočtu klesá. Možným ale komplikovaným řešením by bylo vyvinutí zvláštního mechanismu mutací, který by bral v úvahu nestejnou váhu jednotlivých bitů v řetězcích. Naštěstí se ukazuje, že parametry získané již za relativně krátkou dobu, jsou již obvykle dobrou startovací sadou pro další minimalizaci klasickými postupy.
Jazyk Matlab se díky své schopnosti pracovat s maticemi a dalším zabudovaným funkcím a mechanismům ukazuje pro naprogramování naší metody jako velmi vhodný. Například u genetického algoritmu je možné provádět většinu operací na celé generaci najednou a srovnání teoretické a experimentální závislosti lze uskutečnit jediným příkazem. Navíc prvky všech matic jsou jenom jedničky a nuly. Binární aritmetika ale zatím není používána.
Vzhledem k našemu cíli, kdy není smyslem dovést minimalizaci do konce, kódujeme každý parametr jen osmi bity. Při rozpětí jednoho řádu to znamená 4% přesnost, což se jeví jako dostatečné. Výhodou takového kódování je, že vede k přijatelné délce bitových řetězců.
Pro křížení používáme volitelný počet rodičů dvou pohlaví. Každá matka má právě jednoho potomka s každým otcem a děděné bity od každého z nich se určují při každém křížení náhodně. Při vývoji naší metody jsme také zkoušeli použít ke křížení více než dvou pohlaví. Ukázalo se však, že stejného konečného efektu lze dosáhnout se dvěma pohlavími a dostatečným počtem řetězců v generaci. Takovým způsobem je to asi proto zařízeno v přírodě.
Právě křížení lze pomocí maticového počtu realizovat velice jednoduše. Připraví se matice matek, kde se každá vyskytuje tolikrát, kolik je otců a střídají se ihned po sobě. Podobně se připraví matice otců, ve které se každý vyskytuje po sobě tolikrát, kolik je matek. Každá z těchto matic se logicky po prvcích vynásobí jednou z dvojice disjunktních náhodně vygenerovaných matic, jejichž součet je matice jedničková. Tyto matice řídí, které bity se dědí od kterého rodiče.
Mutace ovládáme pomocí matice, ve které poloha jedniček odpovídá místům, kde dojde v generaci k přepnutí bitů. Přitom hustotu jedniček, obvykle velmi malou, lze řídit jedním parametrem a jejich konkrétní poloha se určuje v každé iteraci náhodně. Tento mechanismus nebere v úvahu fakt, že bity v generaci nemají stejnou váhu. Velikost skoku v konfiguračním prostoru při přepnutí jediného bitu závisí na tom, o který bit se konkrétně jedná. V našem případě ponecháváme skoky relativně velké. Přitom se program při skoku, kdy došlo ke zhoršení nevrací, ale pamatuje si nejlepší zásah.
Výsledná rutina je univerzální pro většinu problémů. Jejím vstupem je jméno testovací funkce, sloupcová matice krajních bodů rozpětí fitovaných parametrů a matice parametrů, které řídí počet rodičů, počet iterací, míru mutací a kreslení průběžných hodnot. Funkce sama připraví kódování a uskuteční minimalizaci s příslušnou délkou a počtem řetězců. Po předepsaném počtu iterací vrací nejlepší parametry, které nalezla.
Na metodu genetického algoritmu navazuje minimalizace pomocí funkce fmins, která je součástí Matlabu. Ta využívá nejlepší předchozí hodnoty jako své vstupní startovací parametry.
Ilustrace použití kombinované metody
Použití metody ilustrujeme na třech příkladech. První a druhý jsou z oblasti zpracování dat maloúhlového rozptylu rentgenového záření s časovým rozlišením a třetí je fitování dat z měření reflektivity na pevných látkách.
Maloúhlový rozptyl rtg. záření obecně nese informaci o velikosti, tvaru a vnitřní struktuře nehomogenit rozptylové hustoty, které mají tzv. koloidní rozměr. Zvláště v případě měření s časovým rozlišením je fyzikální realita velice složitá na to, aby ji bylo možné vystihnout jediným modelem. Kvalita dat navíc klesá s rostoucím časovým rozlišením a obecně je nízká. Obvyklým postupem je problém rozdělit na části, vypočítat jisté diferenciální a integrální parametry pro každou rozptylovou křivku a v dalším kroku sledovat jejich vývoj v čase.
Na obr. 1. jsou data vystihující časový vývoj kvadrátu rozdílu rozptylové hustoty amorfní a krystalické fáze. Jsou výsledkem podílu dvou jiných experimentálních závislostí, a proto je jejich kvalita velice nízká. Bez snahy o podrobné vysvětlení mechanismů je ale zřejmé, že proces krystalizace probíhá ve dvou stupních, které se liší rychlostí. K jejich charakterizaci by zde stačilo nafitovat lineární lomenou funkci. To se je vzhledem k značnému rozptylu dat normálními metodami nemožné. Použitím metody genetického algoritmu je již po několika iteracích proložení sice málo kvalitní pro přesný popis chování, ale dostatečné jako vstupní data pro další minimalizaci, která již vede spolehlivě k požadovaným parametrům.
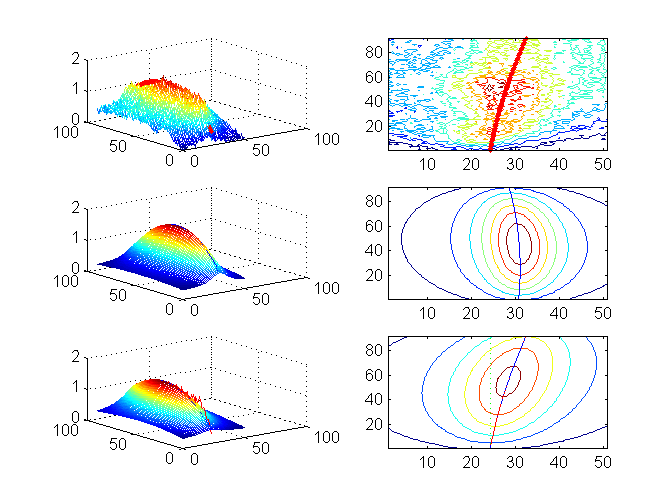
Na obr. 2. je ilustrováno dvojrozměrné fitování vlastností jednoho píku maloúhlového rozptylu rtg. záření v závislosti na čase přímo z experimentálních dat. Vlastnosti píku se ne zcela přesně parametrizují pomocí Lorentzovy funkce. Uvažuje-li se oblast, ve které se vyskytuje pík jediný, lze časovou změnu popsat rovnicí
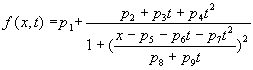
Zde je p1 konstantní pozadí, p2, p3, p4 popisuje parabolické chování velikosti, p5, p6, p7 parabolický pohyb polohy a p8, p9 lineární závislost šířky píku v čase. Z těchto parametrů mají zvláště ty, které popisují pohyb polohy píku zřejmý smysl a mohou být zdrojem fyzikálně zajímavé informace o mezirovinných vzdálenostech v krystalické struktuře. Interpretace změny velikosti a šířky píku je obecně složitější a vypovídá o kvalitě uspořádání.
Vzhledem k počtu a neprůhlednosti parametrů je spolehlivý odhad startovací sady nemožný. Nicméně se opět ukazuje, že naše metoda poskytuje dobrou, i když ne dokonalou, představu o chování píku
Poslední ilustrace na obr. 3. ukazuje fitování měření reflektivity. Zde existuje pro popis vyhovující model se čtyřmi parametry. Jejich hodnoty jsou ale rozdílné v rozpětí mnoha řádů, navíc jejich působení je velmi složité a málo průhledné. Stanovit startovací sadu parametrů je opět prakticky nemožné. Metoda genetického algoritmu přesto dokáže tuto startovací sadu spolehlivě najít. A to i přes to, že apriori jsou známy jenom řádové odhady parametrů.
Závěr
Byla vyvinuta minimalizační metoda založena na výpočtu startovací sady parametrů pomocí metody genetického algoritmu. Tato metoda se ukazuje efektivní v případech, kdy není možné tuto startovací sadu jednoduše a spolehlivě najít, ale je známo rozpětí hodnot, kterých může každý parametr nabývat. Je to ilustrováno na třech typických příkladech.
Poděkování
Na tomto místě bychom rádi poděkovali Grantové agentuře ČR za podporu v rámci grantu č. 109/99/0557
[1] D. E. Goldberg, "Genetic Alghoritms in Search, Optimisation and Machine Learning", Adison-Wesley, Reading, MA. (1989)
[2] M. Steinhart, M.Kriechbaum, M. Horký, J. Baldrian, H. Amenitsch, P. Laggner and S. Bernstorff, "Time-resolved SAXS measurements of effects induced by variation of pressure", Materials Structure in Chemistry, Biology, Physics and Technology, in press
Obr.1: 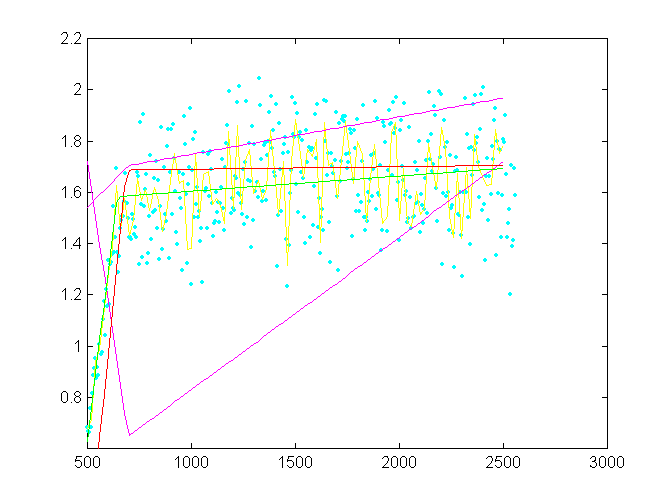 Fit lineární-lomené funkce na data z maloúhlového rozptylu s časovým rozlišením. Modré body jsou experimentální data. Žlutě jsou data vyhlazená pomocí splinů. Tento krok není nutný ale zkrátí výpočet, přičemž rozdíly v parametrech jsou nepatrné. Fialově jsou nástřely při metodě GA. Zobrazují se jen při zlepšení fitu. Červeně je nejlepší z nich, jehož parametry se používá jako startovací sada pro další vypřesnění. Metoda GA zde používá 14 párů rodičů, 10 iterací a velké mutace. Zeleně je celkový fit pomocí funkce fmins. Tento fit je při opakovaní výpočtu shodný na tři platné číslice.
Fit lineární-lomené funkce na data z maloúhlového rozptylu s časovým rozlišením. Modré body jsou experimentální data. Žlutě jsou data vyhlazená pomocí splinů. Tento krok není nutný ale zkrátí výpočet, přičemž rozdíly v parametrech jsou nepatrné. Fialově jsou nástřely při metodě GA. Zobrazují se jen při zlepšení fitu. Červeně je nejlepší z nich, jehož parametry se používá jako startovací sada pro další vypřesnění. Metoda GA zde používá 14 párů rodičů, 10 iterací a velké mutace. Zeleně je celkový fit pomocí funkce fmins. Tento fit je při opakovaní výpočtu shodný na tři platné číslice.
Kontaktní adresa: stein@imc.cas.cz